Hierarchical clustering using SciPy

Overview:

Agglomerative clustering starts with individual nodes of a dataset consisting of n-dimensional data-points. Each individual node of the dataset is considered a cluster. The algorithm works on a bottom-up approach and creates a hierarchy. Based on a criterion or an objective function two nodes are merged together to form a cluster. A newly formed cluster is further merged into an individual node or a cluster.The clustering process is continued by merging smaller clusters until the whole data is merged as a single cluster.

The linkage() function of the cluster.hierarchy module performs agglomerative clustering and creates hierarchical clusters.

The linkage() function of SciPy:

• The linkage() function accepts data-points or distances between them (a.k.a a distance matrix) (scipy.spatial.distancematrix()) and returns a linkage matrix. The linkage matrix describes how the data is clustered and how they are connected as a hierarchy.

• The hierarchy of clusters can be visualized by feeding the linkage matrix to graph routines like the dendrogram() function of hierarchy module to get a dendrogram.

• Many methods are supported by the linkage() function in determining which two clusters are to be merged that include single, complete, average, weighted, centroid, median and Ward”s methods.

The linkage matrix:

• The linkage matrix describes how the hierarchical cluster is formed.

• It is a two dimensional array containing four columns. Everytime a cluster is formed a row is addded to the linkage matrix.

• A cluster can be formed by linking

  • a node with another node

  • a cluster and with another node

  • a cluster with another cluster.

• The first entry and the second entry of a row in the linkage matrix are the indices of the clusters linking which another cluster is formed. These indices can point to a singleton node or a cluster.

• The third entry of the row is the distance between two clusters which is called the the inter-cluster distance.

• The fourth entry is the number of elements present in the resultant cluster. The number of elements in the cluster will be two when just two individual data-points are merged.The number of elements in the cluster will be greater than two, when the merging involves linking with another cluster.

• When the index values(i.e., the first and the second entry of a row) in the linkage matrix exceeds the maximum index of the data-points, it means the index is referring to a cluster formed earlier iterations of the agglomerative clustering, rather than an individual node. The linkage of such cluster is given by linkageIndex = index – len(data_points), which can be traced to an earlier row of the linkage matrix.

Hierarchical clustering using the Single linkage nearest point algorithm:

• When the method of clustering is chosen as “single”, pair-wise distances are calculated and the pair with minimal distance between them is linked as a cluster.

• At subsequent iterations to calculate the distance between a cluster consisting of elements (e1, e2) and a node n1, the minimal distance between (e1, n1) and (e2, n1) is selected.

• The above linking process continues connecting pairs with minimal distance until all the points are connected into a single cluster.

The process can be visualized by plotting pair-wise distances between points using distance matrices describing the distances between all the data-points involved.

The SciPy functions cdist() and distance_matrix() can be used to generated such matrices from a Python program.

SciPy provides an optimized implementation of the single linkage nearest point algorithm using minimum spanning trees.

Example:

Output-Dendrogram:

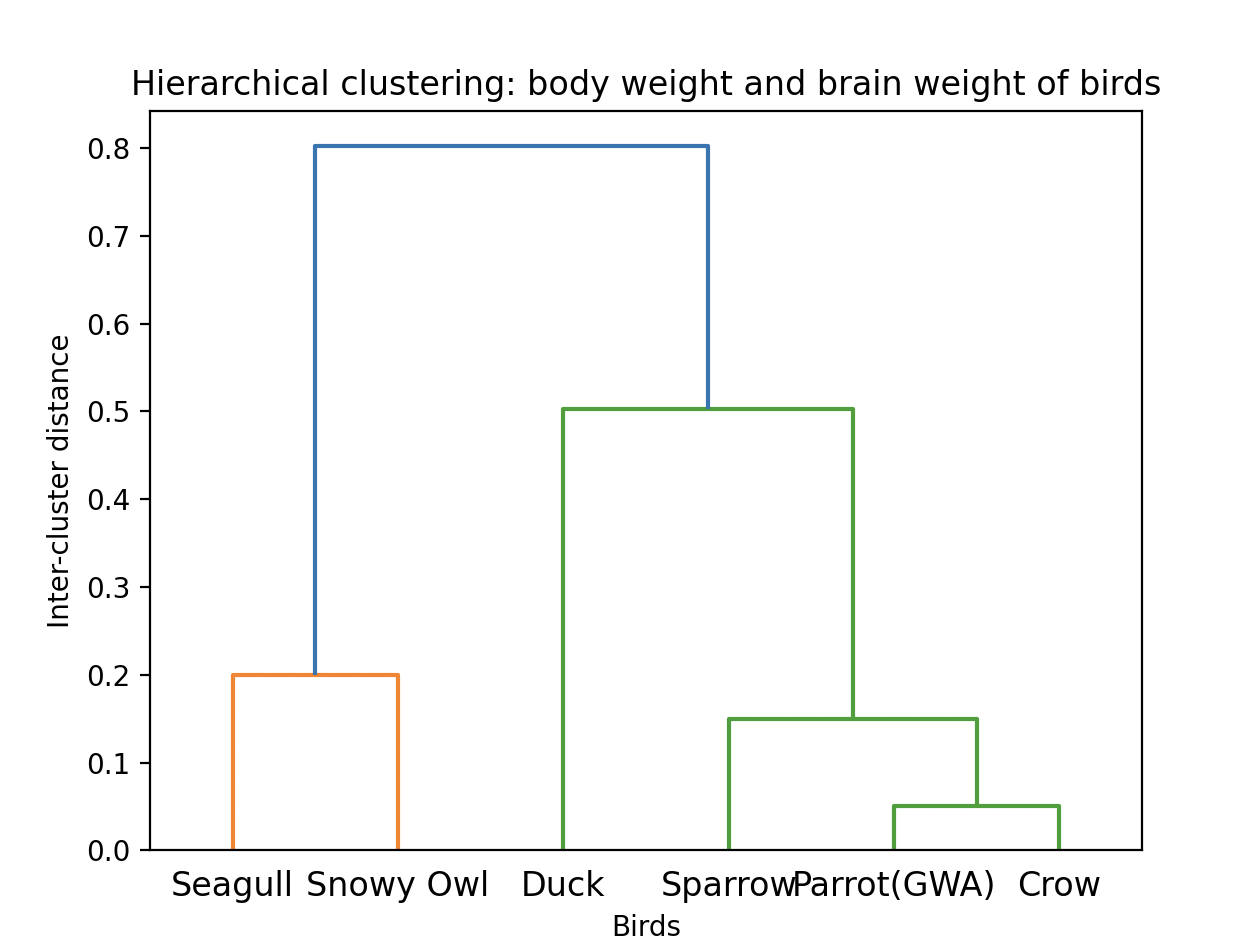
Output-Linkage matrix:

Distance Matrix after iteration 1:

The minimum distance is between the indexes one and two. The elements correspond to the indices are Parrot and Crow. They are merged into a cluster. The inter-cluster distance is 0.05040794. The number of items in the cluster are two.

Distance Matrix after iteration 2:

The minimum distance is found between the cluster formed in the last step and the index corresponding to the item Sparrow. Hence at this step the cluster has the items (Parrot, Crow and Sparrow). The inter-cluster distance is 0.15013015. The number of items in the cluster are Three.

Min(0.15013015, 1.30000105,1.50002324,0.50262991,1.50004033,1.7001297,0.70291963,0.20024984,

0.8017537,1.00092407) = 0.15013015

Distance Matrix after iteration 3:

At this iteration the indexes corresponding to the elements Seagull and Snowy owl are connected and a cluster is formed. The inter-cluster distance is found to be 0.20024984. The number of elements in the cluster is 2. This cluster is not connected yet to the cluster formed in the previous step.

Min(1.30000105, 1.50002324, 0.50262991, 0.20024984, 0.8017537, 1.00092407) = 0.20024984

Distance Matrix after iteration 4:

At this iteration the distance between the cluster consisting of parrot, crow and snowy owl and the index pointing to the element duck is found to be the minimum which is 0.50262991. Hence the inter-cluster distance is 0.50262991. The number of items in the resultant cluster is four with the items Parrot, Crow, Sparrow and Duck.

Min(1.30000105, 0.50262991,0.8017537) = 0.50262991

Distance Matrix after iteration 5:

At the end of this iteration the clusters consisting of elements Parrot, Crow, Sparrow, Duck are connected with the cluster containing Seagull, Snowy owl. The inter-cluster distance is 0.8010537.

Min(1.30000105, 1.35000836, 1.50004033, 0.8017537, 1.50002324, 1.55007018, 1.7001297, 1.00092407) = 0.8010537

The inter-cluster distance of the two clusters linked on each iteration is given at the end of each distance matrix. This inter-cluster distance is provided in the third column of the linkage matrix returned by the scipy linkage() function.