Finding kurtosis for a pandas.series

Overview:

Kurtosis is a statistical measure that describes the peakedness of the curve of a distribution. It is defined as the fourth central moment divided by the standard deviation.
When the distribution is thin and tall it is called a Leptokurtic distribution.
When the distribution is Leptokurtic both of the following things happen:
- Large number of small deviations from the mean
- Large number of large deviations from the mean
In Investment, an asset with Leptokurtic returns can mean higher probability for extremely low or extremely high returns and associated higher value at risk.
When the distribution is less peaked or flatter than the normal distribution, it is called Platykurtic distribution. In a Platykurtic distribution, the tail of the distribution is extremely thin with outliers less than that of the normal distribution.
When the distribution is Mesokurtic the curve resembles that of a normal distribution curve.

Finding Kurtosis for a pandas Series:

The class Series from the Python library pandas implements a one-dimensional collection with several statistical and mathematical functions for Data Analysis.
Series.kurtosis() function computes the Fisher’s kurtosis or Excess Kurtosis for the data present in the series. As per Fisher’s kurtosis - A leptokurtic distribution has a Kurtosis value greater than 0, a normal distribution or a mesokurtic distribution has a Kurtosis value of 0 and a Platykurtic distribution has a Kurtosis value smaller than 0. Kurtosis can be calculated for pandas.DataFrame columns and rows as well.

Example 1:

The Fisher’s Kurtosis value found for the pandas.Series instance in this example is greater than 0 and hence the distribution present in the Series is Leptokurtic.

# Python example program to compute kurtosis of

# the distribution represented by a pandas.Series

import pandas as pds

# Percentage returns from the investment on an asset

returns = [3,3,10,3,5,4,5,10,4]

# Create pandas.Series instance

series = pds.Series(returns)

print("Kurtosis:")

print(round(series.kurtosis(), 2))

Output:

Kurtosis:

0.18 Example 2:

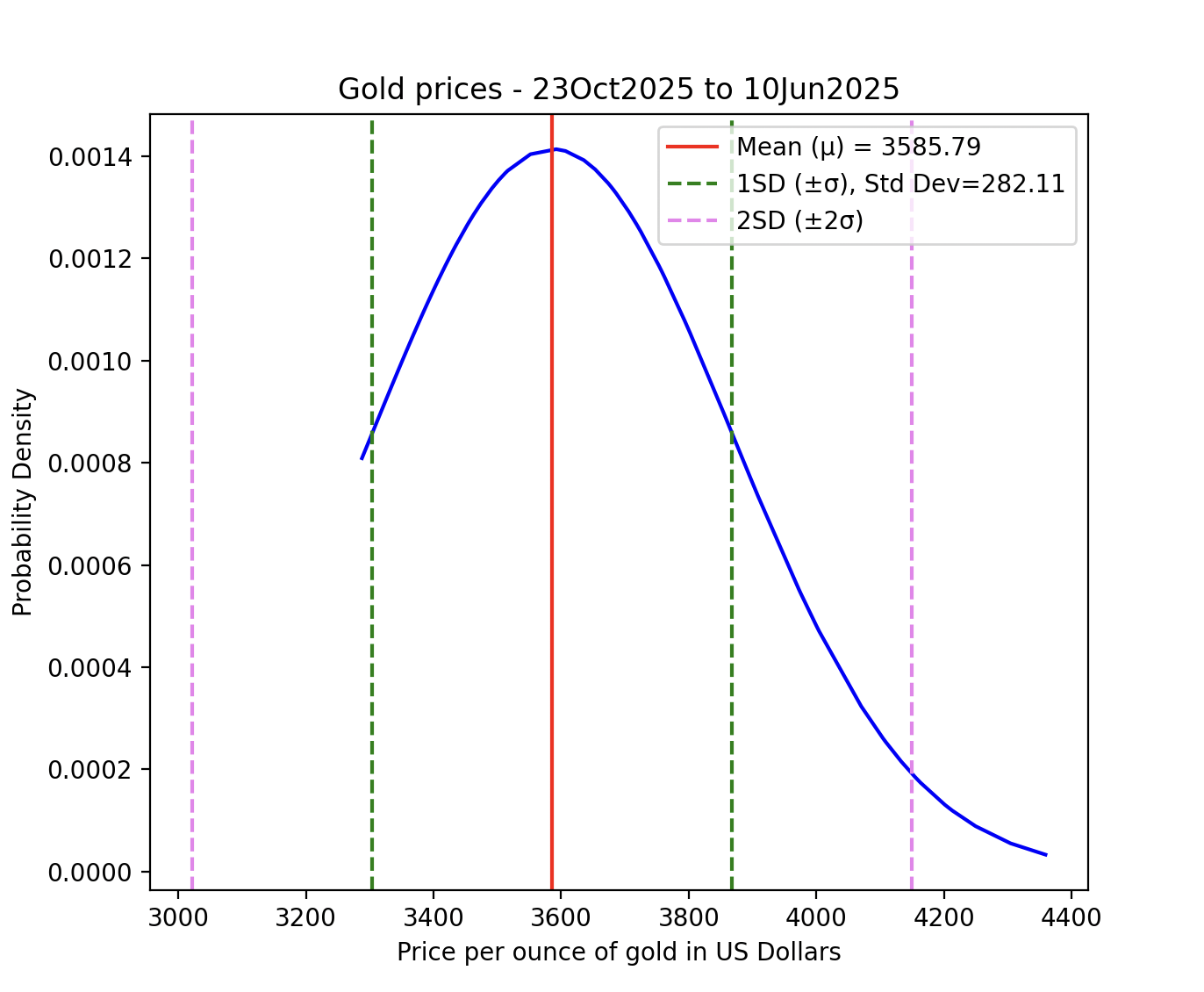
# Example Python program that creates a normal curve
# for the gold price per ounce for 100 days between 23Oct2025
# and 10Jun2025. Gold prices had a tremendous bull market
# in this time period which is reflected in the normal curve
# which is positively skewed and having a leptocurtic kurtosis.
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
import pandas as pds

# 100 days gold prices per ounce
goldPrices =[4154.86, 4104.61, 4109.10, 4359.40, 4249.69, 4213.30, 4304.60, 4201.60,
4163.40, 4133.00, 4000.40, 3972.60, 4070.50, 4004.40, 3976.30, 3908.90,
3868.10, 3897.50, 3873.20, 3855.20, 3793.90, 3756.50, 3753.40, 3801.80,
3761.60, 3705.80, 3678.30, 3717.80, 3725.10, 3719.00, 3686.40, 3673.60,
3682.00, 3682.20, 3677.40, 3653.30, 3606.70, 3635.50, 3592.20, 3551.82,
3512.00, 3516.10, 3474.30, 3435.70, 3420.10, 3404.90, 3418.50, 3381.60,
3388.50, 3358.70, 3378.00, 3382.60, 3383.20, 3408.30, 3399.00, 3404.70,
3491.30, 3453.70, 3433.40, 3434.70, 3426.40, 3399.80, 3348.60, 3352.80,
3368.30, 3354.00, 3392.50, 3431.10, 3455.10, 3501.80, 3462.90, 3358.30,
3345.30, 3359.10, 3336.70, 3359.10, 3364.00, 3325.70, 3321.00, 3316.90,
3342.80, 3346.50, 3342.90, 3359.70, 3349.80, 3307.70, 3287.60, 3333.90,
3329.00, 3320.00, 3380.60, 3385.70, 3384.97, 3408.10, 3406.90, 3417.30,
3452.80, 3402.40, 3343.70, 3343.40]
series = pds.Series(goldPrices)
print("Kurtosis:")
print(round(series.kurtosis(), 2))

goldPrices = np.sort(goldPrices)
mean = np.mean(goldPrices)
std_dev = np.std(goldPrices)

# Compute the probability distribution function of the normal distribution
y = norm.pdf(goldPrices, loc = mean, scale = std_dev)

# Plot the normal curve
plt.plot(goldPrices, y, color = 'blue')
plt.axvline(mean, color='red', linestyle='solid',
label=f'Mean (μ) = {mean:.2f}')

# Draw vertical on both sides of the mean
# defining 1 standard deviation away from the mean
plt.axvline(mean + std_dev, color='green', linestyle='--',
label=f'1SD (±σ), Std Dev={std_dev:.2f}')
plt.axvline(mean - std_dev, color='green', linestyle='--')

# Draw vertical on both sides of the mean
# defining 2 standard deviation away from the mean
plt.axvline(mean + 2 * std_dev, color='violet', linestyle='--',
label=f'2SD (±2σ)')
plt.axvline(mean - 2 * std_dev, color='violet', linestyle='--')

# Give a title
plt.title('Gold prices - 23Oct2025 to 10Jun2025')
plt.xlabel('Price per ounce of gold in US Dollars')
plt.ylabel('Probability Density')

# Display the legends
plt.legend()

# Display the plot
plt.show()

Output:

Kurtosis:
0.07

Positively skewed and leptokurtic

Example 3:

The Fisher’s Kurtosis value found for the pandas.Series instance in this example is less than 0 and hence the distribution present in the Series is Platykurtic.

# Python example program to compute kurtosis of

# the distribution represented by a pandas.Series

import pandas as pds

# Values of a distribution

vals = [2,2.2,2.3,2.1,1.9,2.3]

# Create pandas.Series instance

series = pds.Series(vals)

print("Kurtosis:")

print(round(series.kurtosis(), 2))

Output:

Kurtosis:

-1.48