SciPy hierarchical clustering using complete-linkage

Overview:

The single-linkage algorithm and the complete linkage algorithm both work in similar ways. Both of them use the minimum distance between clusters while combining them into another cluster. The difference lies when calculating the inter-cluster distance between a cluster with more than one node and a cluster with one or more number of nodes.

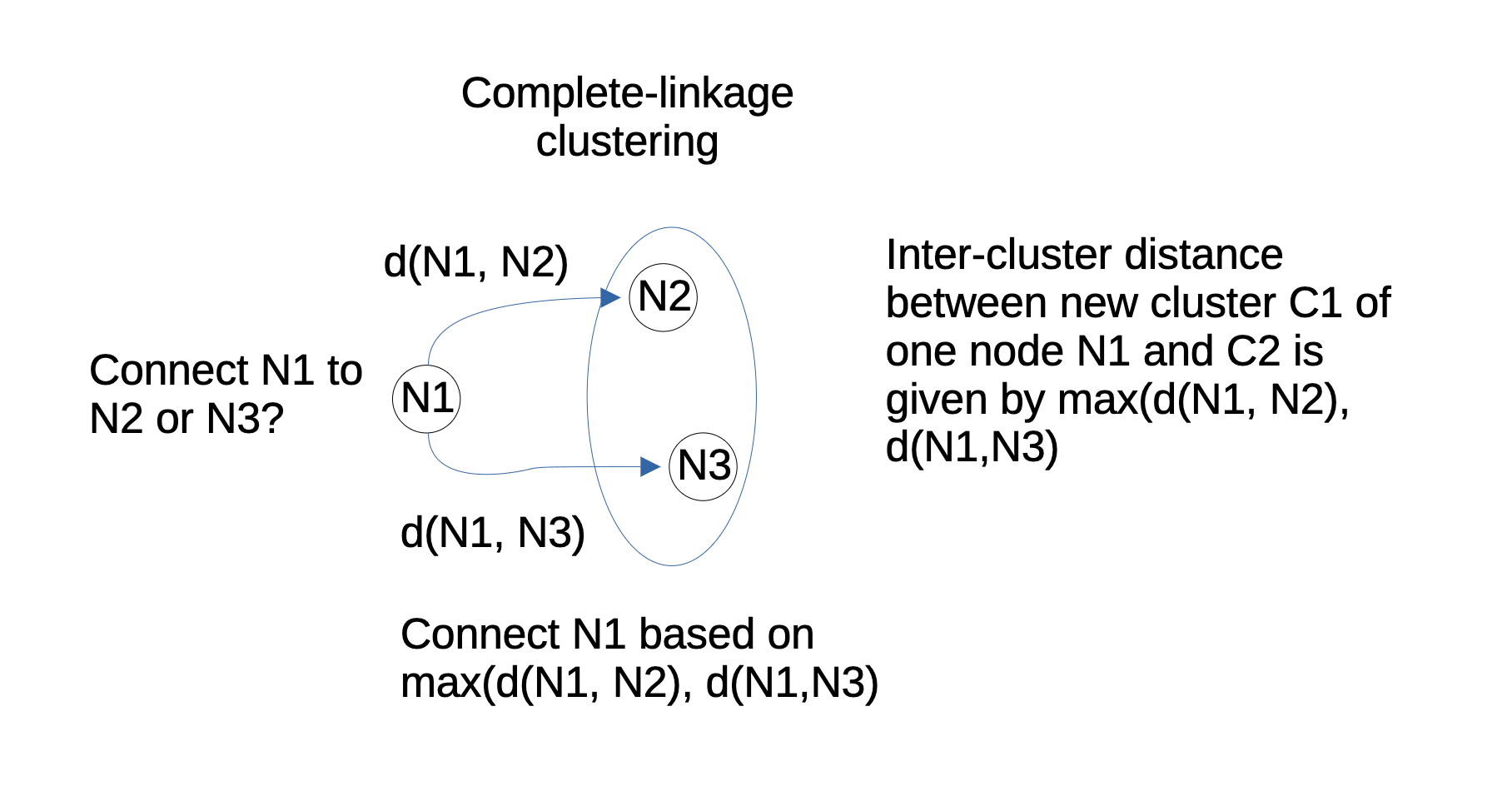
In complete-linkage, to calculate the inter-cluster distance between a cluster with nodes (e1, e2) and another cluster (e3, e4) the maximum of distance(e1, e3), distance(e1, e4), distance(e2, e3) and distance(e2, e4) is selected. This is the reason for the algorithm to be called as farthest neighbour algorithm.

While neighbours are always nearby entities, the single-linkage algorithm selects the nearest neighbour and the complete linkage algorithm selects the farthest neighbour.

Example:

The Python code to perform hierarchical clustering using the complete-linkage method is same as the single-linkage example, except for the invocation of the linkage() function. The linkage() function invocation has to be modified with “complete” for the parameter “method” as given here:

The invocation of scipy linkage() function using the method “complete” performs agglomerative hierarchical clustering through the complete-linkage algorithm.

The data-points are the same as used in the example for hierarchical clustering through single-linkage. For the given data-points though the resultant clusters and the dendogram look the same for both single-linkage and complete-linkage methods the order in which these clusters are created and linked differ. 

Output - The linkage matrix:

Distance matrix after iteration 1:

At this iteration the pair of data-points with minimal distance between them is linked together to form the first cluster. The cluster consists of indexes 0 and 1 of the ndarray which refer to the elements Parrot and Crow.

Inter-cluster distance = 0.05040794.

Distance matrix after iteration 2:

At this iteration the indexes three and four are linked together to form a cluster. These indexes refer to the elements Seagull and Snowy Owl. The inter-cluster distance is 0.20024984. The number of items in the cluster is two. When compared with single-linkage algorithm the clustering order differs as the selection criteria for the neighbour changes.

Min(0.20039966, 1.35000836, 1.55007018, 0.55302356, 1.50004033, 1.7001297, 0.70291963, 0.20024984, 0.8017537, 1.00092407) = 0.20024984

Distance matrix after iteration 3:

At this iteration the cluster formed at iteration one and the index two are linked together which adds the element Sparrow to the cluster containing Parrot and Crow. The inter-cluster distance is 0.20039966 which is given by maximum(distance (parrot, sparrow), distance (crow and sparrow).

Min(0.20039966, 1.55007018, 0.55302356, 1.7001297, 0.70291963, 1.00092407) = 0.20039966

Distance matrix after iteration 4:

At this iteration index 5 is linked to the cluster formed at the iteration 3. The index of the linkage matrix corresponding to the iteration 3 is 8 as given by the fourth row of the linkage matrix. To get the actual index on the linkage matrix this value has to be subtracted from the number of data-points. Actual index = value - length(data points) 

Min(1.7001297, 0.70291963, 1.00092407) = 0.70291963

Distance matrix after iteration 5: